Kao SciPy je otvoreni izvor, ima vrlo aktivnu i živu zajednicu programera zbog čega postoji ogroman broj modula za veliku količinu znanstvenih aplikacija i proračuna dostupnih sa SciPy. Neke od složenih matematičkih operacija koje se mogu izvesti pomoću SciPy-a su:
- Interpolacija
- Integracija
- Optimizacija
- Obrada slike
- Statistika
- Izračuni posebne funkcije itd.
SciPy se može usporediti s većinom naredbenih i standardnih knjižnica poput GSL biblioteke za C ++ i Matlab. Kako je SciPy izgrađen na vrhu NumPy paketa, ova dva paketa mogu se u potpunosti integrirati. Ako se možete sjetiti matematičke operacije koju treba obaviti, provjerite SciPy knjižnicu prije nego što samostalno implementirate taj modul, jer u većini slučajeva SciPy već ima sve operacije za vas koje su u potpunosti implementirane.
Instalirajte SciPy knjižnicu
Instalirajmo SciPy knjižnicu prije nego što prijeđemo na stvarne primjere i koncepte. Postoje dva načina za instalaciju ovog paketa. Prva uključuje upotrebu upravitelja paketa Python, pip:
pip instalirati scipyDrugi se način odnosi na Anacondu, paket možemo instalirati kao:
conda install -c anaconda scipyNakon što se knjižnica instalira, možemo je uvesti kao:
uvoz scipyKonačno, budući da ćemo koristiti i NumPy (preporučuje se da za sve NumPy operacije koristimo NumPy izravno umjesto da prolazimo kroz SciPy paket):
uvoz numpyMoguće je da ćemo u nekim slučajevima također voljeti ucrtati svoje rezultate za koje ćemo koristiti Matplotlib knjižnicu. Izvršite sljedeći uvoz za tu knjižnicu:
uvoz matplotlibZa sve primjere u ovoj lekciji koristit ću upravitelja Anaconde. Pokrenut ću Jupyter bilježnicu za isti:

Sad kad smo spremni sa svim naredbama za uvoz napisati neki kôd, krenimo s ronjenjem u SciPy paket s nekoliko praktičnih primjera.
Rad s polinomnim jednadžbama
Započet ćemo razmatranjem jednostavnih polinomnih jednadžbi. Postoje dva načina na koja možemo integrirati polinomske funkcije u naš program. Možemo se koristiti poly1d klasa koja koristi koeficijente ili korijene polinoma za inicijalizaciju polinoma. Pogledajmo primjer:
iz numpy uvoza poly1dfirst_polynomial = poly1d ([3, 4, 7])
ispis (prvi_polinom)
Kada pokrenemo ovaj primjer, vidjet ćemo sljedeći izlaz:

Jasno je da je polinomni prikaz jednadžbe ispisan kao izlaz, tako da je rezultat prilično lako razumljiv. Možemo izvoditi razne operacije i na ovom polinomu, poput kvadrata, pronaći njegovu izvedenicu ili čak riješiti za vrijednost x. Pokušajmo učiniti sve ovo u sljedećem primjeru:
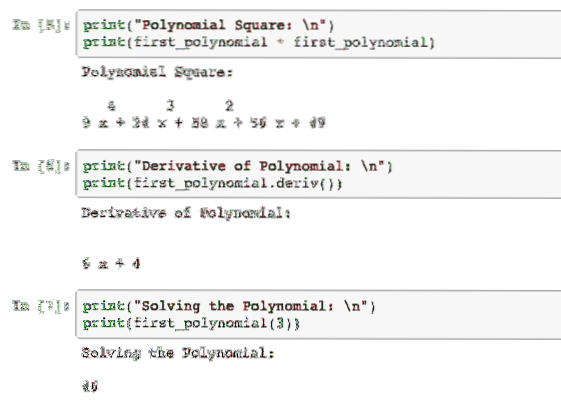
ispis ("Polinomski kvadrat: \ n")ispis (prvi_polinom * prvi_polinom)
ispis ("Derivat polinoma: \ n")
ispis (prvi_polinom.deriv ())
print ("Rješavanje polinoma: \ n")
ispis (prvi_polinom (3))
Kada pokrenemo ovaj primjer, vidjet ćemo sljedeći izlaz:
Taman kad sam razmišljao da je to sve što možemo učiniti sa SciPyem, sjetio sam se da možemo integrirati i polinom. Izvršimo posljednji primjer s Polinomima:
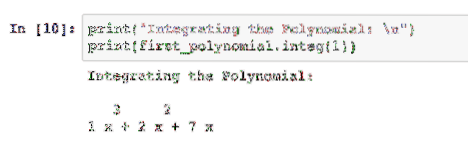
print ("Integriranje polinoma: \ n")ispis (prvi_polinom.integ (1))
Cijeli broj koji prolazimo govori paketu koliko puta treba integrirati polinom:
Jednostavno možemo dodati još jedan cijeli broj koji paketu govori koliko puta treba integrirati ovaj polinom.
Rješavanje linearnih jednadžbi
Moguće je čak riješiti linearne jednadžbe sa SciPyjem i pronaći njihove korijene, ako postoje. Da bismo riješili linearne jednadžbe, skup jednadžbi predstavljamo kao NumPy nizove i njihovo rješenje kao zasebne NumPy nizove. Vizualizirajmo to na primjeru u kojem činimo isto i koristimo se linalg paket za pronalaženje korijena jednadžbi, evo jednadžbi koje ćemo rješavati:
1x + 5y = 63x + 7y = 9
Riješimo gornje jednadžbe:
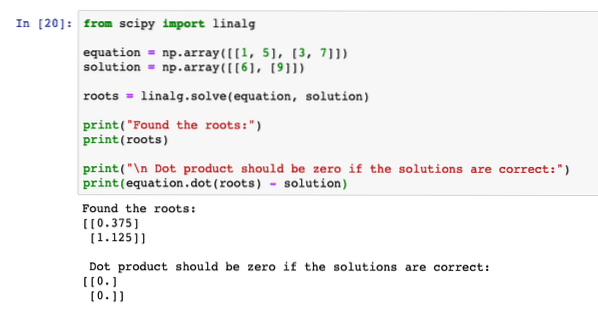
od scipy import linalgjednadžba = np.niz ([[1, 5], [3, 7]])
rješenje = np.niz ([[6], [9]])
korijenje = linalg.riješiti (jednadžba, rješenje)
print ("Pronašli korijene:")
ispis (korijeni)
print ("\ n Točkasti proizvod treba biti nula ako su rješenja točna:")
ispis (jednadžba.točka (korijeni) - rješenje)
Kada pokrenemo gornji program, vidjet ćemo da jednadžba točkanog proizvoda daje nulti rezultat, što znači da su korijeni koje je program pronašao bili točni:
Fourierove transformacije sa SciPyjem
Fourierove transformacije pomažu nam da izrazimo funkciju kao zasebne komponente koje čine tu funkciju i vodi nas kroz način na koji možemo rekombinirati te komponente kako bismo vratili izvornu funkciju.
Pogledajmo jednostavan primjer Fourierovih transformacija gdje crtamo zbroj dva kosinusa pomoću Matplotlib biblioteke:
od scipyja.fftpack uvoz fft# Broj uzoraka
N = 500
# razmak uzorka
T = 1.0/800.0
x = np.Linspace (0.0, N * T, N)
y = np.jer (50.0 * 2.0 * np.pi * x) + 0.5 * np.jer (80.0 * 2.0 * np.pi * x)
yf = fft (y)
xf = np.Linijski prostor (0.0, 1.0 / (2.0 * T), N // 2)
# matplotlib za svrhe crtanja
uvoz matplotlib.pyplot kao plt
plt.zaplet (xf, 2.0 / N * np.trbušnjaci (yf [0: N // 2]))
plt.naslov ('Informacije')
plt.ylabel ('Y os')
plt.xlabel ('X os')
plt.rešetka ()
plt.pokazati()
Ovdje smo započeli s konstrukcijom jednadžbe prostora i kosinusne jednadžbe koju smo zatim transformirali i ucrtali. Evo rezultata gornjeg programa:
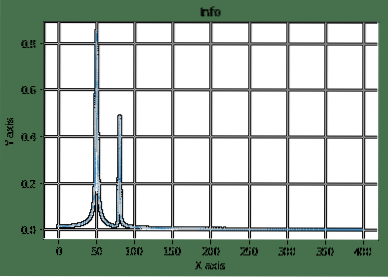
Ovo je jedan od dobrih primjera gdje vidimo kako se SciPy koristi u složenoj matematičkoj jednadžbi za jednostavnu vizualizaciju stvari.
Vektori i matrica sa SciPyjem
Sad kad znamo puno stvari za što je SciPy sposoban, možemo biti sigurni da SciPy može raditi i s vektorima i matricom. Matrice su važan dio linearne algebre jer su matrice nešto što koristimo i za predstavljanje vektorskih preslikavanja.
Baš kao što smo gledali na rješavanje linearnih jednadžbi sa SciPy, tako i vektore možemo predstaviti s np.niz () funkcije. Počnimo s konstruiranjem matrice:
moja_matrica = np.matrica (np.slučajno.slučajno ((3, 3)))ispis (my_matrix)
Evo rezultata gornjeg isječka:

Kad god govorimo o matricama, uvijek govorimo o vlastitim vrijednostima i vlastitim vektorima. Jednostavnije rečeno, vlastiti vektori su vektori koji, pomnoženi matricom, ne mijenjaju smjer, za razliku od većine vektora. To znači da čak i kada pomnožite vlastite vektore s matricom, postoji vrijednost (ili vlastita vrijednost) koja je jedan od faktora množenja. To znači:
Sjekira = λx.U gornjoj jednadžbi A je matrica, λ je vlastita vrijednost, a x vektor. Napišimo jednostavan isječak koda kako bismo pronašli vlastite vrijednosti za zadati Vektor:
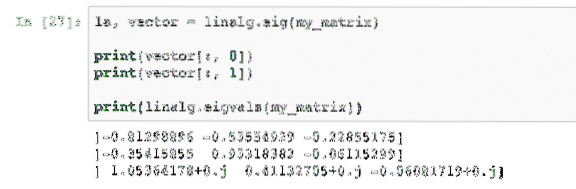
la, vektor = linalg.eig (moja_matrica)ispis (vektor [:, 0])
ispis (vektor [:, 1])
tisak (linalg.eigvals (my_matrix))
Kada pokrenemo ovaj primjer, vidjet ćemo sljedeći izlaz:
Izračunata matrična odrednica
Sljedeća operacija koju ćemo izvršiti sa SciPy je izračunavanje odrednice dvodimenzionalne matrice. Ponovno ćemo upotrijebiti matricu koju smo koristili u posljednjem isječku koda ovdje:
linalg.det (moja_matrica)Kada pokrenemo ovaj primjer, vidjet ćemo sljedeći izlaz:

Zaključak
U ovoj smo lekciji pogledali puno dobrih primjera u kojima nam SciPy može pomoći izvodeći složena matematička izračunavanja za nas s API-jem i paketima koji se lako koriste.
 Phenquestions
Phenquestions