Kôd ovog bloga, zajedno sa skupom podataka, dostupan je na sljedećoj poveznici https: // github.com / shekharpandey89 / k-znači
K-Means klasterizacija je nenadgledani algoritam strojnog učenja. Ako usporedimo algoritam K-Means nenadgledanog klasteriranja s nadgledanim algoritmom, nije potrebno trenirati model s označenim podacima. K-Means algoritam koristi se za klasificiranje ili grupiranje različitih objekata na temelju njihovih atributa ili značajki u K broj grupa. Ovdje je K cjelobrojni broj. K-Means izračunava udaljenost (koristeći formulu udaljenosti), a zatim pronalazi minimalnu udaljenost između podatkovnih točaka i centroidne skupine za klasifikaciju podataka.
Razumijemo K-sredstva koristeći mali primjer pomoću 4 objekta, a svaki objekt ima 2 atributa.
| ObjectsName | Atribut_X | Atribut_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-Sredstva za rješavanje numeričkog primjera:
Da bismo riješili gornji numerički problem putem K-Meana, moramo slijediti sljedeće korake:
K-Means algoritam je vrlo jednostavan. Prvo moramo odabrati bilo koji slučajni broj K, a zatim odabrati centroide ili središte nakupina. Za odabir centroida možemo odabrati bilo koji slučajni broj objekata za inicijalizaciju (ovisi o vrijednosti K).
Osnovni koraci algoritma K-Means su sljedeći:
- Nastavlja se izvoditi dok se nijedan objekt ne pomakne sa svojih centroida (stabilno).
- Prvo odabiremo neke centroide nasumično.
- Zatim određujemo udaljenost između svakog objekta i centroida.
- Grupiranje objekata na temelju minimalne udaljenosti.
Dakle, svaki objekt ima dvije točke kao X i Y, a na prostoru grafikona predstavljaju sljedeće:
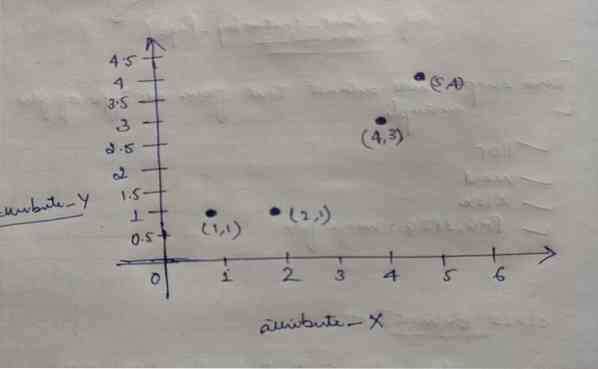
Stoga u početku biramo vrijednost K = 2 kao slučajnu da bismo riješili naš gornji problem.
Korak 1: U početku odabiremo prva dva objekta (1, 1) i (2, 1) kao svoje centroide. Grafikon u nastavku prikazuje isto. Te centroide nazivamo C1 (1, 1) i C2 (2,1). Ovdje možemo reći da je C1 grupa_1, a C2 grupa_2.
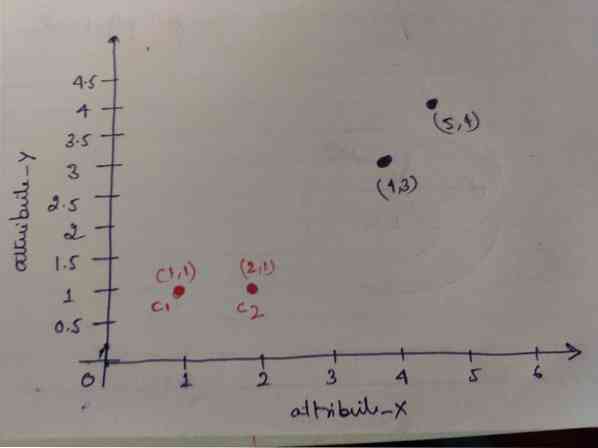
Korak 2: Sada ćemo izračunati svaku točku podataka objekta prema centroidima koristeći euklidsku formulu udaljenosti.
Za izračunavanje udaljenosti koristimo sljedeću formulu.

Izračunavamo udaljenost od predmeta do centroida, kao što je prikazano na donjoj slici.

Dakle, izračunali smo udaljenost svake točke podataka o objektu pomoću gore navedene metode udaljenosti, napokon smo dobili matricu udaljenosti kao što je dato u nastavku:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) nakupina1 | grupa_1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) nakupina2 | grupa_2 |
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | x |
| 1 | 1 | 3 | 4 | Y |
Sada smo izračunali vrijednost udaljenosti svakog objekta za svaki centroid. Na primjer, objektne točke (1,1) imaju vrijednost udaljenosti do c1 je 0 i c2 je 1.
Kako iz gornje matrice udaljenosti doznajemo da objekt (1, 1) ima udaljenost do nakupine 1 (c1) 0, a do nakupine 2 (c2) 1. Dakle, objekt jedan je blizu samog klastera1.
Slično tome, ako provjerimo objekt (4, 3), udaljenost do nakupine 1 je 3.61, a klasteru 2 je 2.83. Dakle, objekt (4, 3) prebacit će se u nakupinu2.
Slično tome, ako provjerite postoji li objekt (2, 1), udaljenost do klastera 1 je 1, a do klastera 2 0. Dakle, ovaj će se objekt prebaciti na cluster2.
Sada, prema njihovoj vrijednosti udaljenosti, grupiramo točke (grupiranje objekata).
G_0 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | grupa_1 |
| 0 | 1 | 1 | 1 | grupa_2 |
Sada, prema njihovoj vrijednosti udaljenosti, grupiramo točke (grupiranje objekata).
I na kraju, grafikon će izgledati dolje nakon izvršavanja klasteriranja (G_0).
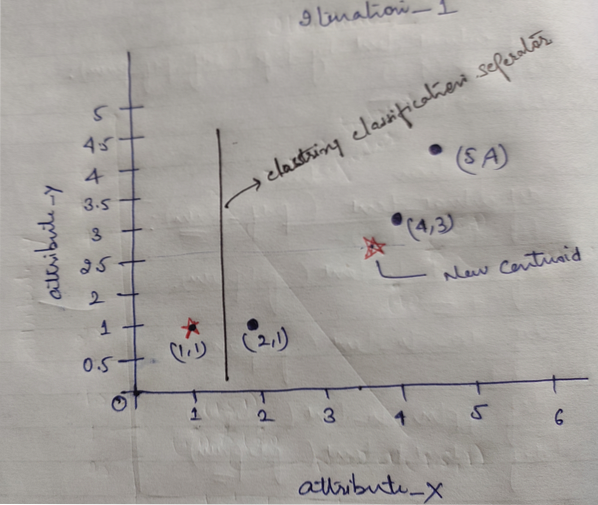
Ponavljanje_1: Sada ćemo izračunati nove centroide kako su se mijenjale početne skupine zbog formule udaljenosti kako je prikazano u G_0. Dakle, group_1 ima samo jedan objekt, tako da je njegova vrijednost i dalje c1 (1,1), ali group_2 ima 3 objekta, tako da je njegova nova centroid vrijednost 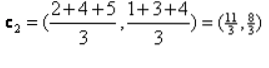
Dakle, novi c1 (1,1) i c2 (3.66, 2.66)
Sada opet moramo izračunati svu udaljenost do novih centroida kao što smo računali prije.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) nakupina1 | grupa_1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) nakupina2 | grupa_2 |
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | x |
| 1 | 1 | 3 | 4 | Y |
Iteracija_1 (grupiranje objekata): Sada ga, u ime izračuna nove matrice udaljenosti (DM_1), grupiramo prema tome. Dakle, premještamo objekt M2 iz grupe_2 u grupu_1 kao pravilo minimalne udaljenosti do centroida, a ostatak objekta bit će isti. Tako će novo grupiranje biti kao u nastavku.
G_1 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | grupa_1 |
| 0 | 0 | 1 | 1 | grupa_2 |
Sada moramo ponovno izračunati nove centroide, jer oba objekta imaju dvije vrijednosti.
Dakle, novi centroidi će biti 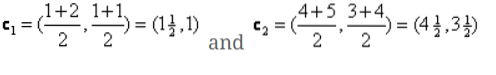
Dakle, nakon što dobijemo nove centroide, grupiranje će izgledati dolje:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
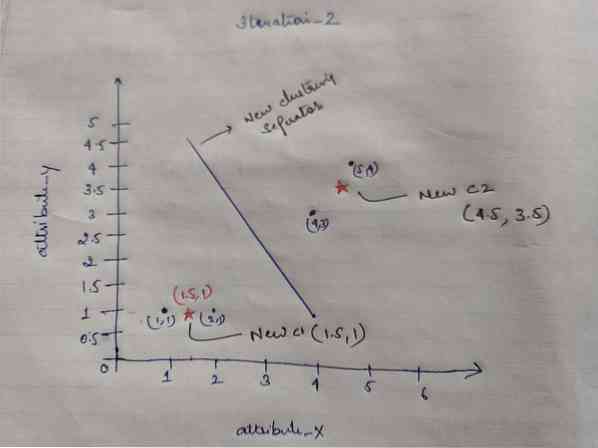
Ponavljanje_2: Ponavljamo korak u kojem izračunavamo novu udaljenost svakog objekta do novih izračunatih centroida. Dakle, nakon izračuna dobit ćemo sljedeću matricu udaljenosti za iteraciju_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) nakupina1 | grupa_1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) nakupina2 | grupa_2 |
A B C D
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | x |
| 1 | 1 | 3 | 4 | Y |
Opet, dodijeljivanje klastera radimo na temelju minimalne udaljenosti kao i prije. Dakle, nakon što smo to učinili, dobili smo matricu klasteriranja koja je ista kao G_1.
G_2 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | grupa_1 |
| 0 | 0 | 1 | 1 | grupa_2 |
Kao ovdje, G_2 == G_1, tako da nije potrebna daljnja iteracija, i ovdje možemo stati.
K-znači implementacija pomoću Pythona:
Sada ćemo implementirati algoritam K-znači u python. Da bismo implementirali K-sredstva, koristit ćemo poznati Iris skup podataka, koji je otvoren izvor. Ovaj skup podataka ima tri različite klase. Ovaj skup podataka ima u osnovi četiri značajke: Duljina čašice, širina čašice, duljina latica i širina latice. Posljednji stupac reći će naziv klase tog retka poput setosa.
Skup podataka izgleda kao u nastavku:
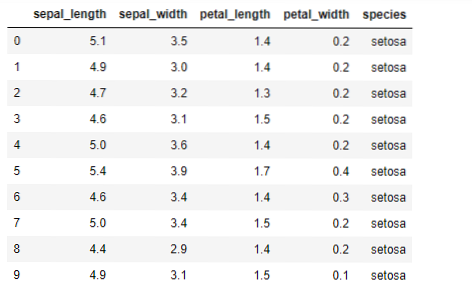
Za implementaciju python k-znači, moramo uvesti potrebne knjižnice. Tako uvozimo Pande, Numpy, Matplotlib, a također i KMeans iz sklearna.gomilač kako je navedeno u nastavku:

Čitamo Iris.csv skup podataka koristeći metodu read_csv pande i prikazat će 10 najboljih rezultata metodom head.
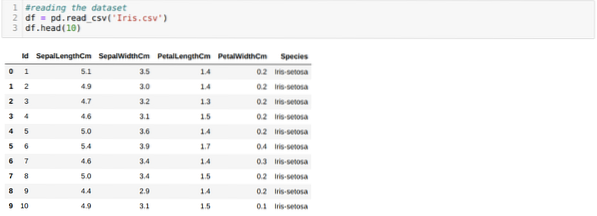
Sada čitamo samo one značajke skupa podataka koje su nam trebale za osposobljavanje modela. Dakle, čitamo sve četiri značajke skupova podataka (duljina traka, širina čašica, duljina latica, širina latica). Za to smo proslijedili četiri vrijednosti indeksa [0, 1, 2, 3] u funkciju iloc podatkovnog okvira pande (df) kako je prikazano dolje:
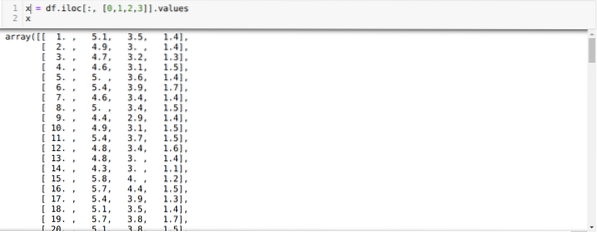
Sada slučajnim odabirom broja klastera (K = 5). Stvaramo objekt klase K-sredstva, a zatim uklapamo svoj x skup podataka u onaj za trening i predviđanje kao što je prikazano u nastavku:
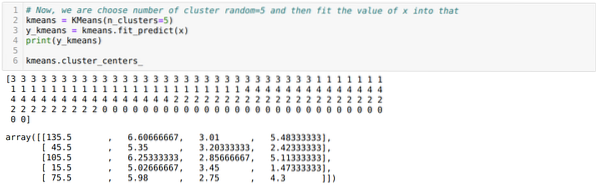
Sada ćemo vizualizirati naš model sa slučajnom vrijednošću K = 5. Jasno možemo vidjeti pet nakupina, ali čini se da nije točno, kao što je prikazano u nastavku.
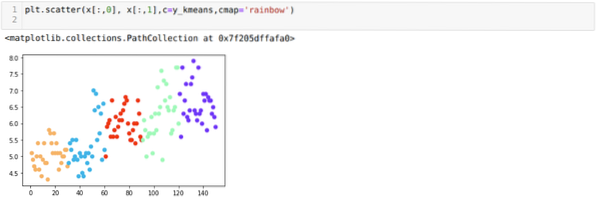
Dakle, naš sljedeći korak je saznati je li broj klastera bio točan ili ne. A za to koristimo metodu Lakat. Metoda Elbow koristi se za pronalaženje optimalnog broja klastera za određeni skup podataka. Ovom će se metodom utvrditi je li vrijednost k = 5 bila točna ili nije jer ne dobivamo jasno klasteriranje. Dakle, nakon toga idemo na sljedeći graf koji pokazuje da vrijednost K = 5 nije točna jer optimalna vrijednost pada između 3 ili 4.
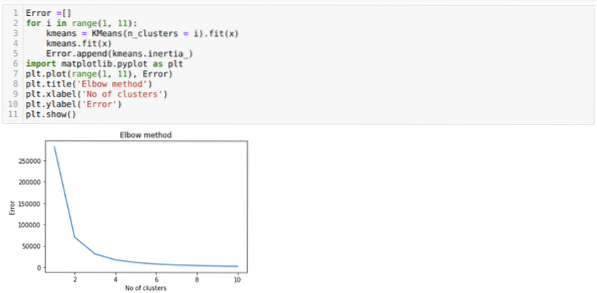
Sada ćemo ponovo pokrenuti gornji kod s brojem klastera K = 4, kao što je prikazano dolje:
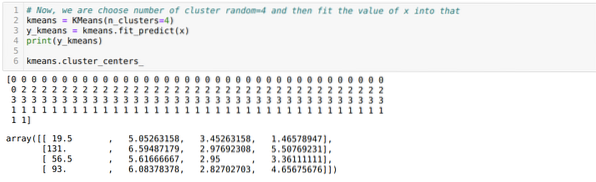
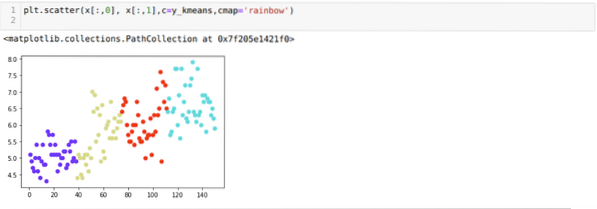
Sada ćemo vizualizirati gornju K = 4 klasterizaciju nove gradnje. Zaslon dolje pokazuje da se sada grupiranje vrši putem k-sredstava.
Zaključak
Dakle, proučavali smo algoritam K-sredina i u numeričkom i u python kodu. Također smo vidjeli kako možemo saznati broj klastera za određeni skup podataka. Ponekad metoda Lakat ne može dati točan broj nakupina, pa u tom slučaju postoji nekoliko metoda koje možemo odabrati.
 Phenquestions
Phenquestions


